SiC熱分解法によるグラフェン結晶成長
グラフェンが電子材料として注目を浴びている他の理由として、従来の半導体技術との親和性がよい、というものが挙げられる。グラフェンは2次元シート状であるため、リソグラフィによる微細加工、二次元的なコンタクト電極やゲート電極等のデバイス構造の作り込みが可能である。実際、Novoselov 以来、測定されたデバイスの多くが、表面に300nmほどの厚さの SiO2 層を持った Si 基板上に、リソグラフィなどを使って作り込まれたものである[1]。ただし、肝心のグラフェンは、グラファイトをメンディングテープで剥離し、剥離したグラフェンを SiO2 上に転写することによって作られており、この方法は実に簡便でこの分野の発表が爆発的に増加した原因ではあるが、デバイス応用を考えた場合は実用的でない。引き上げインゴットから基板を作るシリコンやあるいは化合物半導体のエピタキシャル成長基板のように、広範囲にグラフェンで覆われた基板自体を効率よく作り出す必要がある。
そうした技術の中で有望視されているものの一つが、SiC 基板上のエピタキシャルグラフェン成長技術である。 Si の融点(1420˚C)は C の融点(約4500˚C)よりもずっと低いので、SiC 基板を高温(1000˚C 以上)で熱すると Si が表面から脱離蒸発し、C 過剰となる。常圧で安定な C の作る結晶相はダイヤモンドでなくグラファイトであるので、この過剰となった C が表面で凝集することによりグラファイトが表面にできる。この際、成長層の厚さを制御してやれば、1層のシートであるグラフェンを作成することもできるのである。実際この基板を用いたデバイスが早い時期からデモンストレーションされている[2]。また、我々は SiC の表面に何層のグラフェンが成長しているかを実空間で判別できる顕微鏡技術を立ち上げたが、それによるとうまく制御すれば基板 SiC のステップの上を越えて mm 角のオーダーでつながった欠陥のない均一な厚さのグラフェンを成長することが可能であることがわかっている[3]。
しかし、均一で質の良いグラフェン基板を得るには、まだ課題が多い。そもそもどのようにグラフェンが成長しているかがわかっていない。高温アニールによりSiC の表面は表面のSi 被覆率が減少しC 被覆率が増加して、 ( √3 × √3 )R30˚ 表面再構成相、( 6 √3 × 6 √3 )R30˚ 表面再構成相を経て、1 層、2 層とグラフェンが成長した表面へ変化する[4]。問題はグラフェンがどこからどのように成長してくるのかが、わかっていないことにある。そもそも、SiC が表面で分解してグラフェンシートができているので、グラフェン層一層を作るのに 3 bilayer のSiC が分解しないといけない。この際、Si が表面から脱離し、過剰な C が凝集する必要がある。
通常の半導体のエピタキシャル成長とのアナロジーを考えれば最表面に新しいグラフェン層が成長しているはずであるが、グラフェンシート間が弱いファンデルワールス相互作用でしか結合していないので、もしそうであれば成長したグラフェンの配向が基板と良い整合性を示す必然性はない。また、グラフェンシートはエッジを持つはずであるが、これがどのようになっているのかもよくわかっていない。ステップが重要な役割をしていることも考えられるのだが、我々の断面 TEM の実験によればグラフェンシートはステップで不連続ではなく、つながったままステップの上を越えている[5]。界面の原子構造も問題で、グラフェンと基板の間にバッファ層と呼ばれる層があり、これが ( 6 √3 × 6 √3 )R30˚ 表面再構成相と同じような原子構造を持っているようなのだが、その詳細は特定されていない。
そこで我々は第一原理計算により、 SiC(0001)面上のグラフェン成長機構についての検討を進めた[6]。問題を単純化して、C 原子の被覆率が増えていったときにSiC 上でCがどのように凝集するのかを調べてみたところ、理想Si 表面上ではC は凝集してグラフェンを形成するのがエネルギー的に安定であることがわかった。しかも、基板表面がグラフェンシート1層ですでに覆われている場合には、グラフェンの表面でなく基板との界面に凝集する方が安定で、その後グラフェンシートへも成長できることが示された。このことはグラフェンシートの成長が界面で起こっている可能性を示唆している。
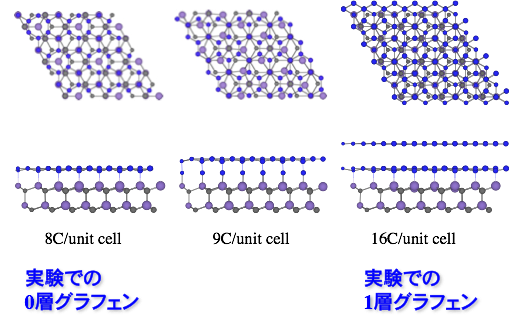
これまでの様々な第一原理計算研究者の検討により、SiC 基板の理想Si 表面をグラフェンシート1層で覆った場合、その表面構造は6 √3 × 6 √3 の再構成を取ることが知られている[7-9]。そして、この1層で覆った表面の電子構造は Dirac cone を全く示さず、さらにもう1層グラフェンシートを載せないと Dirac cone が現れないことがわかっている。つまり、SiC 基板の理想Si 表面をグラフェンシート1層で覆った構造(1GL)は実験で観測されている 6 √3 × 6 √3 のバッファ層の原子構造(0ML)に対応し、グラフェンシート2層以上のn 層で覆った構造 (nGL)が実験で観測されている (n–1) 層のグラフェンの成長した表面 ((n–1)ML) に対応すると考えられる。とすると、我々の結果は、常に第 0 層に当たるシートが界面から成長していると考えられることを示している。成長するシートの配向が自然と基板と整合するし、SiC が界面で分解することで C は供給されるので、この考え方は妥当と思われるが、余剰となった Si がどうなったのかや、表面のステップの役割はどうなっているかなど、これから解明すべき課題は多い。
1) K. S. Novoselov, A. K. Geim, S. V. Morozov, D. Jiang, Y. Zhang, S. V. Dubonos, I. V. Grigorieva, and A. A. Firsov, Science 306, 666 (2004).
2) C. Berger, Z. Song, X. Li, X. Wu, N. Brown, C. Naud, D. Mayou, T. Li, J. Hass, A. N. Marchenkov, E. H. Conrad, P. N. First, and W. A. de Heer, Science 312, 1192 (2006).
3) H. Hibino, H. Kageshima, F. Maeda, M. Nagase, Y. Kobayashi, and H. Yamaguchi, Phys. Rev. B 77, 075413 (2008).
4) A. Fissel, Phys. Rep. 379, 149 (2003).
5) M. Nagase, H. Hibino, H. Kageshima, and H. Yamaguchi, Nanotechnology 20, 445704 (2009).
6) H. Kageshima, H. Hibino, M. Nagase, and H. Yamaguchi, Appl. Phys. Exp. 2, 065502 (2009).
7) A. Mattausch and O. Pankratov, Phys. Rev. Lett. 99, 076802 (2007).
8) F. Varchon, J. Hass, X. Li, N. Nguyen, C. Naud, P. Mallet, J. Y. Veuillen, C. Berger, E. H. Conrad, and L. Magaud, Phys. Rev. Lett. 99, 126805 (2007).
9) S. C. Kim, J. S. Ihm, H. J. Choi, and Y. W. Son, Phys. Rev. Lett. 100, 176802 (2008).





