グラフェンの移動度とキャリア散乱
グラフェンが電子材料として注目を浴びた理由は、なんといってもその移動度の高さである。Novoselov らによって最初に報告された際にすでに室温以下では温度によらず10000cm2/Vs であり、コヒーレンス長は0.4μm にも及んだ[1]。
グラフェンのキャリアの運動は、相対論的な粒子として取り扱うことが必要である。電子が頻繁に散乱される拡散領域における電流を考える場合には、しかし別に難しいことではなく、なじみの深い光子を考えてみれば良い。光子の衝突は、運動量
を持つ粒子として扱われる[2]。従って衝突散乱の観点からすると、
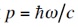
つまり
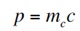
として定義した質量 mc を実効的には持っていることになる。
グラフェンのキャリアに当てはめると、Dirac 点をエネルギーの原点として(ε0 ≡ 0 )フェルミエネルギー εF を測れば
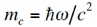
となり、Dirac 点に近いほど軽くなる。
移動度 μ はこの実効質量 mc を用いて
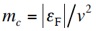
と書ける。従って散乱緩和時間 τ が εF によらないのであれば、グラフェンでは μ は |εF| に反比例して Dirac 点に近いほど大きくなるが、キャリア密度 n が |εF| の2乗に比例するので伝導率
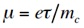
は |εF| に比例してDirac 点に近いほど小さくなる。この古典論的取り扱いは、Diracキャリアとして厳密に扱った議論と一致する。
しかし、Novoselov らによって報告されたグラフェンの伝導率 σ は、Dirac 点極近傍を除いて n にほぼ比例すると言うものであり[1]、 μ が |εF| によらずほぼ一定、つまり τ が |εF| に比例するような散乱機構によって伝導が律速されていることを意味していた。そのような散乱はリモートクーロン散乱であり[2,3]、グラフェンの表面吸着物やグラフェンを支える基板の SiO2 あるいはその界面の残留物に起因すると考えられる。実際、グラフェンを宙に張り、しかも加熱して表面の吸着物を取り除くことにより、移動度230000cm2/Vs が実現されている[4]。
このようにリモートクーロン散乱が律速になっているのは不純物散乱がほとんど無いからであり[5]、これは半導体ヘテロ界面と同様にグラフェンシート内にドーパントがほとんど全く存在しない純粋な結晶構造をしていることに起因している。グラフェンをデバイスに応用するためには異種材料との界面は欠かせないものであり、リモートクーロン散乱の制御は重要と思われる。実際、グラフェンをh-BNで挟むことで、リモートクーロン散乱の抑制効果があることが報告されている。また、ギャップを開けるためにGNR 化したとするとエッジ散乱へも配慮が必要であろう。しかし、高い移動度だけに着目した従来型FET のチャネル材料としての利用以外にも、その長いコヒーレンス長はスピン干渉デバイスなどの新規デバイスの可能性を期待させるものである[6]。
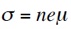
1) K. S. Novoselov, A. K. Geim, S. V. Morozov, D. Jiang, Y. Zhang, S. V. Dubonos, I. V. Grigorieva, and A. A. Firsov, Science 306, 666 (2004).
2) T. Ando, J. Phys. Soc. Jpn. 75, 074716 (2006).
3) K. Nomura and A. H. MacDonald, Phys. Rev. Lett. 96, 256602 (2006).
4) K. I. Bolotin, K. J. Sikes, Z. Jiang, M. Klima, G. Fudenberg, J. Hone, P. Kim, and H. L. Stormer, Solid State Commun. 146, 351 (2008).
5) J.-H. Chen, C. Jang, S. Xiao, M. Ishigami, and M. S. Fuhrer, Nature Nanotechnol. 3, 206
(2008).
6) W. Han, K. Pi, W. Bao, K. M. McCreary, Yan Li, W. H. Wang, C. N. Lau, and R. K. Kawakami,
Appl. Phys. Lett. 94, 222109 (2009).





