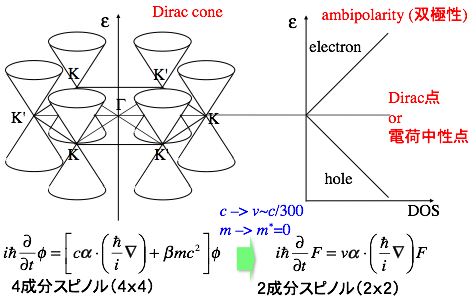
グラフェンの原子構造とバンド構造
グラフェンの原子構造は C が蜂の巣状に並んだ構造であり、正三角形が二つ組み合わさった平行四辺形の形をした二次元単位胞内に、C 原子が二つ存在し、どちらか片方を A サイト(例えば下図白丸)、もう片方を B サイト(例えば下図黒丸)と呼ぶ。A サイトの原子も B サイトの原子も各々は正三角形に並び(三角格子を組み)、相手の正三角形の重心に位置している。 六角形の中心のサイトも正三角形に並んでいるが、ここに C 原子は存在しない。これらの幾何学的特徴は、グラフェンの電子状態を決定する上で重要である[1-3]。
このような蜂の巣状の構造が実現している理由は、C 原子が3本の sp2 の混成軌道を作っていて、それぞれが隣の C 原子との間で強いσ結合を作っている事による。sp2 混成軌道は、 s 軌道、px 軌道、py 軌道から作られ、平面内にお互いの間の角度が 120°をなすように配向しており、これがグラフェンが蜂の巣状の 2 次元シート構造の骨格を保っている源となっ ている。その一方、これらの軌道は強いσ結合を作っているため、C-C 原子間に強く局在していて、エネルギー的にも深く、フェルミエネルギー近傍には現れてこない。フェルミ エネルギー近傍に現れるのは、このσ結合に関与しない、pz 軌道がπ結合することによっ て作られる電子状態、πバンドである。
σ結合はエネルギー的に遙かに深い所にあるので、πバンドは純粋に各 C 原子の上に pz 軌道だけがあると考えて導出することができる。
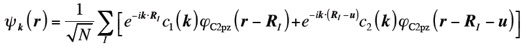
強結合(tight-binding)近似に基づけば、係数c1(k)とc2(k)は次の2行2列の行列固有方程式を
解くことで得られる。
ただし
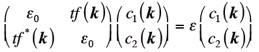
容易に分かるように、この解となる固有エネルギーは
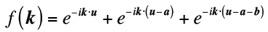
ただし
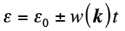
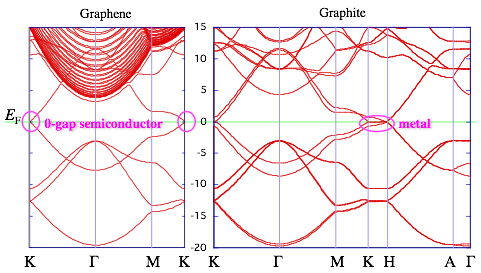
である。電子は単位胞当たりA サイトとB サイトのpz 軌道に一つずつなので、-の符号の方のバンド(結合性πバンド)のみを完全占有し(価電子帯)、+の符号のバンド(反結合性πバンド)は完全に空となる(伝導帯)。ここで注意したいのは、w(k)はK 点でのみ厳密に0 となる事であり、つまり価電子帯と伝導帯のバンドギャップは0 である。また、K点近傍でk の二階偏微分により有効質量を計算してみると、再びK点では厳密に0 となる。
また、価電子帯頂上、伝導帯下底付近に誘起されるキャリアの運動を考えると、K 点近傍では有効質量が0 であるため分散関係は通常のようにk の二次関数にならない。そこで、K点近傍でf(k)をテーラー展開してみる。するとK点近傍でのバンド構造を決める行列固有方程式は、
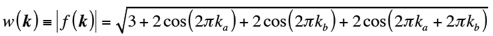
と書かれる。
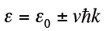
であるから、
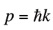
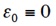
とエネルギーの基準を取れば、これは
と光での
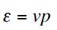
と同じであり、 v が光速 c に当たる。グラフェンの実効光速 v は光の 1/300 程度であるが[4]、K 点近傍でのキャリアの運動には、数学的には従って通常の粒子の運動を記述する Schröinger 方程式でなく、光子の運動を記述する Dirac 方程式を用いる必要がある。
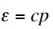
1) A. H. Castro Neto, F. Guinea, N. M. R. Peres, K. S. Novoselov, and A. K. Geim, Rev. Mod. Phys. 81, 109 (2009).
2) T. Ando and T. Nakanishi, J. Phys. Soc. Jpn. 67, 1704 (1998).
3) 「カーボンナノチューブの基礎と応用」, 齋藤理一郎, 篠原久典 編, 培風館 (2004).
4) A. K. Geim and K. S. Novoselov, Nature Materials 6, 183 (2007).
5) M.-Y. Han, B. Özyilmaz, Y. Zhang, and P. Kim, Phys. Rev. Lett. 98, 206805 (2007).
6) S. K. Banerjee, L. F. Register, E. Tutuc, D. Reddy, and A. H. MacDonald, IEEE Electron Dev. Lett. 30, 158 (2009).
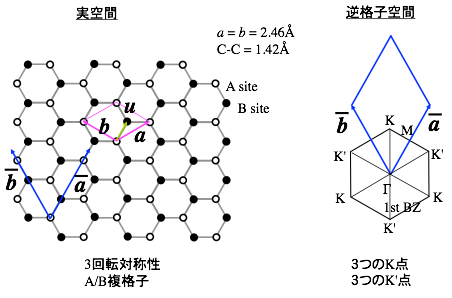
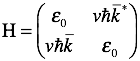
となる。ただし、
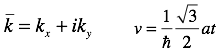
これを解くと、一次関数となって
K点では厳密に 0 となり、K 点近傍ではエネルギーに対して比例して増減、その傾きは価電子帯側、伝導帯側で同じである。 K 点で状態密度が 0 になることから、グラフェンが半導体であることが分かり、バンドギャップが0 であるため、グラフェンは「0 ギャップの半導体」と言える。 これらの性質は、より厳密な第一原理計算によっても再現される。
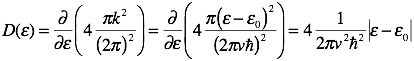
また、「0 ギャプ半導体」であるので、通常の半導体のようにゲート電圧をうまく外部から与えれば、電界効果でフェルミエネルギーεF の位置を容易に「0 ギャップ」点であるDirac 点の上下に変えることができる。通常の半導体のように、Dirac 点より高エネルギーの伝導帯内ではキャリアは負の電荷、低エネルギーの価電子帯内では正の電荷、を持つ。p 型かn 型かをゲート電界だけで制御できる性質を表して「ambipolarity」と呼び、またDirac 点を「電荷中性点」とも呼ぶ。
相対論的Dirac 方程式に従って運動するmassless Fermion というのは、素粒子の世界を別として、固体物理の世界ではこれまで知られていなかった。高エネルギーの世界でなく低エネルギーの半導体の中で観測でき、しかもゲート電圧次第で粒子の密度も荷電の正負も自由自在に制御できる。こうしたことも、グラフェンの物性測定の成功で世界がにわかにざわめきたった理由である。
一方、デバイス応用の観点からすると、「0 ギャップ半導体」、「ambipolarity」、という性質は諸刃の剣である。ゲート電圧によってフェルミエネルギーの位置が自由に変えられるというのはMOSFET としての利用の可能性があるが、エネルギーギャップが0 ということはオフの状態の制御が難しいことを意味しており、使い勝手が悪い。さらにCMOS として使うには、ambipolarity が邪魔である。幅の狭い短冊状の構造(Graphene Nano Ribbon, GNR)として量子閉じ込めサイズ効果でバンドギャップを開けるというのは一つの解であり、30nm 巾で10meV ほどのギャップを開けられることが報告されている[5]。また、多層にするなど、何らかの方法でA サイトとB サイトが等価でない状況を作り出せばバンドギャップを開けられる。一方で、「0 ギャップ半導体」、「ambipolarity」という性質は特異でそれ自身魅力的でもあり、これを積極利用した新規デバイスの可能性を期待させる[6]。

Dirac 方程式は一般的に光速に近い速さで運動する相対論的フェルミオン粒子に用いられる方程式であり、その相対論的な性質を表して「massless Dirac Fermion」と呼ばれる。Dirac 方程式は4成分スピノルの式であるが、質量 m=0 なので2成分スピノルの式に簡略化される。この式はWeyl方程式と呼ばれ、近年質量があることが発見されるまでニュートリノの従う式と考えられてきた。そして、価電子帯と伝導帯が ε = ε0 と重なっている K 点を「Dirac 点」、K 点付近でのバンド分散関係が二つの円錐がK 点を頂点につながった形となっていることを表して「Dirac cone」と称されている。原子構造の対称性から、Dirac 点もDirac cone も第一ブリルアン域内に2種類(K 点とK'点)存在している。
そして状態密度(DOS)を計算してみると、